728x90
에라토스테네스의 체란?
에라토스테네스의 체는 고대 그리스 수학자 에라토스테네스가 발견한 소수를 찾는 방법입니다.
마치 체로 치듯이 소수를 걸러낸다고 하여 '에라토스테네스의 체'라고 불립니다.
소수를 걸러내기 위해 2부터 N까지의 순서로 소수를 찾아 그 숫자의 배수들을 모두 제거하여 제거되지 않은 N까지의 모든 소수를 찾아낼 수 있습니다.
에라토스테네스의 체 적용
1) 우선 다음과 같이 1~100까지의 숫자를 나열합니다.

2) 1인 소수가 아니므로 제거합니다.

3) 2를 제외한 2의 배수를 모두 제거합니다.

4) 3을 제외한 3의 배수를 모두 제거합니다.

5) 5를 제외한 5의 배수를 모두 제거합니다. (4의 배수는 2의 배수에서 이미 제거가 되어서 지울 필요가 없음)
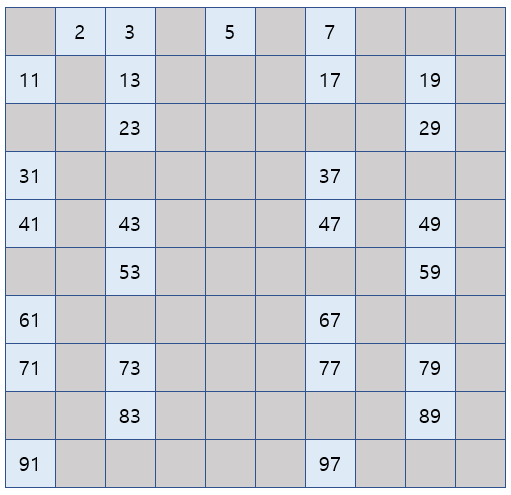
6) 7을 제외한 7의 배수를 모두 제거합니다. (6의 배수도 2의 배수에서 이미 제거됨)
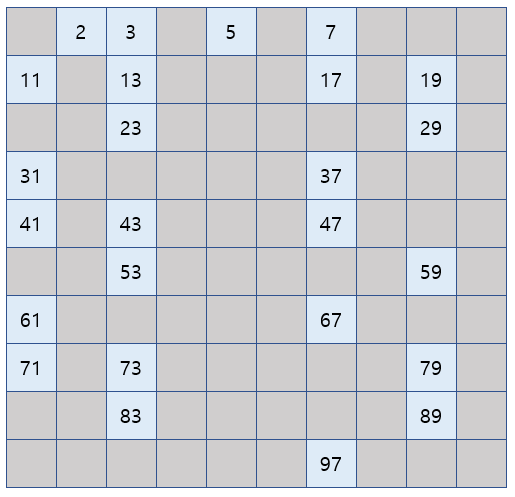
위에 제거되지 않은 수들이 100 이하의 소수입니다. 8의 배수와 9의 배수 그리고 10의 배수는 각각 2의 배수, 3의 배수, 2의 배수에 포함되기 때문에 이미 제거가 된 것입니다. 그리고 11의 배수를 처리하지 않은 이유는 11의 2의 배수부터는 100을 넘어가기 때문에 지울 필요가 없습니다. 일종의 노가다 방식이라 무식한 방법처럼 보이지만, 특정 범위 내에서 모든 소수를 찾는 방법은 에라토스테네스의 체가 가장 빠릅니다.
시간 복잡도는 O(NloglogN)으로 선형 시간에 가까울 정도로 빠르지만, N의 범위만큼의 메모리 할당이 필요하기 때문에 메모리가 많이 필요하다는 단점 또한 가지고 있습니다.
에라토스테네스의 체 구현
코드
# 자연수 n입력
n = int(input())
# 2~n 범위의 리스트 할당
a = [0] * (n+1)
for num in range(2, n+1):
if a[num] == 0:
# 소수이면 출력
print(num, end=' ')
# 배수 소수 처리
for j in range(num, n+1, num):
a[j] = 1
실행 결과

728x90
반응형
'PS > 알고리즘 이론' 카테고리의 다른 글
| [파이썬으로 배우는 알고리즘] 그리디(Greedy) 알고리즘 (0) | 2022.07.18 |
|---|---|
| [파이썬으로 배우는 알고리즘] 비트마스크(BitMask) (0) | 2022.07.15 |
| [파이썬으로 배우는 알고리즘] BFS(너비 우선 탐색) (0) | 2022.07.14 |
| [파이썬으로 배우는 알고리즘] DFS(깊이 우선 탐색) (0) | 2022.07.12 |
| [파이썬으로 배우는 알고리즘] 재귀(Recursion) 알고리즘 (2) | 2022.07.05 |
![[파이썬으로 배우는 알고리즘] 에라토스테네스의 체](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FmgNMG%2FbtrGXgNCQrS%2FXT41jFJoM8cqvgkyQFXS9k%2Fimg.png)