분할정복(Divide & Conquer) 알고리즘이란?
문제 해결에 있어서 어떤 문제를 더이상 쪼갤 수 없을 때까지 분할한 후 (Divide) 하위 문제들을 해결하고 (Conquer) 합치면서(Combine) 문제의 답을 도출하는 알고리즘을 분할정복(Divide & Conquer) 알고리즘이라고 합니다.
설명만으로는 잘 이해가 안 갈 수도 있으니 대표적인 분할정복 문제인 병합정렬(Merge Sort)과 퀵정렬(Quick Sort)을 예시로 직접 풀어보면서 설명하도록 하겠습니다!

병합정렬(Merge Sort)
병합정렬 개념
1) 정렬할 리스트를 더 이상 나눌 수 없을 때까지 2개의 부분 리스트로 분할(Divide)
2) 더이상 나눌 수 없는 부분 리스트를 다시 합치면서 정렬 수행(Conquer, Combine)
병합정렬 과정

1) 두 개의 부분 리스트로 나눔

2) 두 개의 부분 리스트 각각을 또 두 개의 부분 리스트로 나눔

3) 네 개의 부분 리스트 각각을 또 두 새의 부분 리스트로 나눔 (여기까지가 Divide 더 나눌 수 없음)

4) 8개의 부분 리스트를 다시 합치면서 정렬 (Conquer, Combine)

5) 4개의 부분 리스트를 다시 합치면서 정렬 (Conquer, Combine)

6) 2개의 부분 리스트를 다시 합치면서 정렬 (Conquer, Combine)

코드
import sys
input = sys.stdin.readline
def merge_sort(lt, rt):
if lt < rt:
mid = (lt + rt) // 2
# Divide
merge_sort(lt, mid)
merge_sort(mid+1, rt)
# Conquer, Combine
temp = list()
# 나눴던 두 리스트의 시작 인덱스
ls = lt
rs = mid+1
# 비교하며 임시 리스트에 삽입
while ls <= mid and rs <= rt:
if arr[ls] < arr[rs]:
temp.append(arr[ls])
ls += 1
else:
temp.append(arr[rs])
rs += 1
# 둘 중 한 리스트가 임시 리스트에 다 삽입된 경우
# 남은 리스트를 임시 리스트에 삽입
if ls <= mid:
temp = temp + arr[ls:mid+1]
else:
temp = temp + arr[rs:rt+1]
for i in range(lt, rt + 1):
arr[i] = temp[i-lt]
if __name__ == "__main__":
arr = [4, 3, 7, 1, 2, 8, 5, 6]
print("정렬전 리스트: ", end='')
print(arr)
merge_sort(0, 7)
print()
print("병합정렬후 리스트: ", end='')
print(arr)merge_sort() 함수를 재귀적으로 호출합니다. conquer 전에 일단 리스트를 나눠야 하므로 conquer 코드 전에 merge_sort() 함수를 사용해서 리스트를 나눠주도록 하고, 다 분할되면 분할된 리스트들의 인덱스를 사용하여 상위 리스트를 정렬시킵니다.
결과
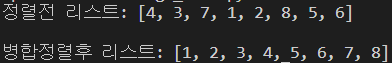
합병정렬은 n개의 데이터로 logn의 단계를 거치기 때문에 최악의 상황에도 O(nlogn)을 보장한다는 장점이 있습니다!
퀵정렬(Quick Sort)
퀵정렬 개념
1) 리스트에서 임의의 값을 기준으로 하고 이것을 pivot이라고 함
2) pivot을 기준으로 pivot보다 작은 값들은 왼쪽에 큰 값들은 오른쪽에 둠
3) pivot을 제외한 리스트에 대해서 위와 같은 작업 반복(Divide)
2) 더 이상 나눌 수 없는 부분 리스트를 다시 합침(Conquer, Combine)
퀵 정렬 과정
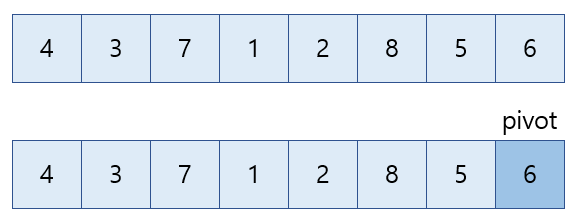
1) 임의로 리스트의 마지막 값을 pivot으로 설정. 6이 pivot이 됨
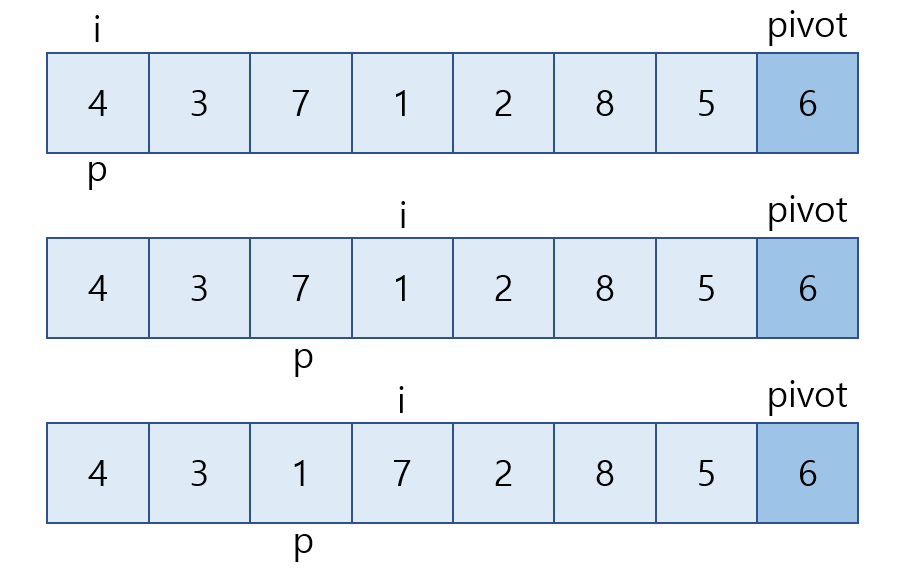
2) pivot을 제외한 리스트를 순회하기 위한 i, 그리고 자리를 바꾸기 위한 p 설정. i가 인덱스를 돌면서 해당 인덱스의 값이 pivot보다 작은 경우만 p에 있는 값과 바꾼 후 p값도 증가시킴. 이렇게 하면 pivot보다 작은 값은 순서를 유지하게 됨.
만약 해당 인덱스의 값이 pivot보다 크면 아무 작업도 하지 않음. 후에 해당 값이 pivot보다 크게 되면 해당 값과 p에 있는 값을 바꿔줌.
위에서 보면 i와 p가 함께 증가하다가 pivot보다 큰 7을 만났기 때문에 p값은 거기서 멈춤. 바로 pivot보다 작은 1을 만나고 둘의 자리를 바꿔줌!!
- i가 0일 때 값은 4이고, 4는 pivot보다 작음 -> p에 해당하는 값과 교체(p에 해당하는 값은 4이므로 변화 없음) 후 p 1증가 -> p값은 1
- i가 1일 때 값은 3이고, 3은 pivot보다 작음 -> p에 해당하는 값과 교체(p에 해당하는 값은 3이므로 변화 없음) 후 p 1증가 -> p값은 2
- i가 2일 때 값은 7이고, 7은 pivot보다 큼
- i가 3일 때 값은 1이고, 1은 pivot보다 작음 -> p에 해당하는 값과 교체(p에 해당하는 값은 7) 후 p 1증가 -> p값은 3
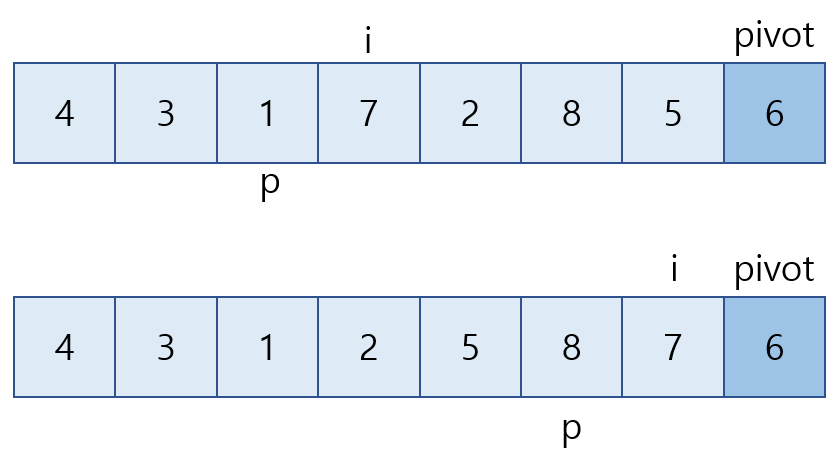
3) 순회를 마치고 나면 i는 pivot 직전에 있고, p는 8이 있는 인덱스에 멈춰있음.
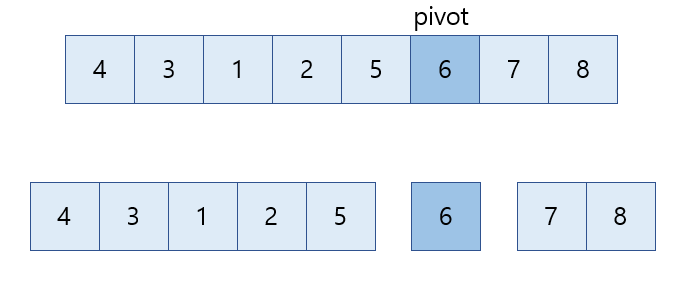
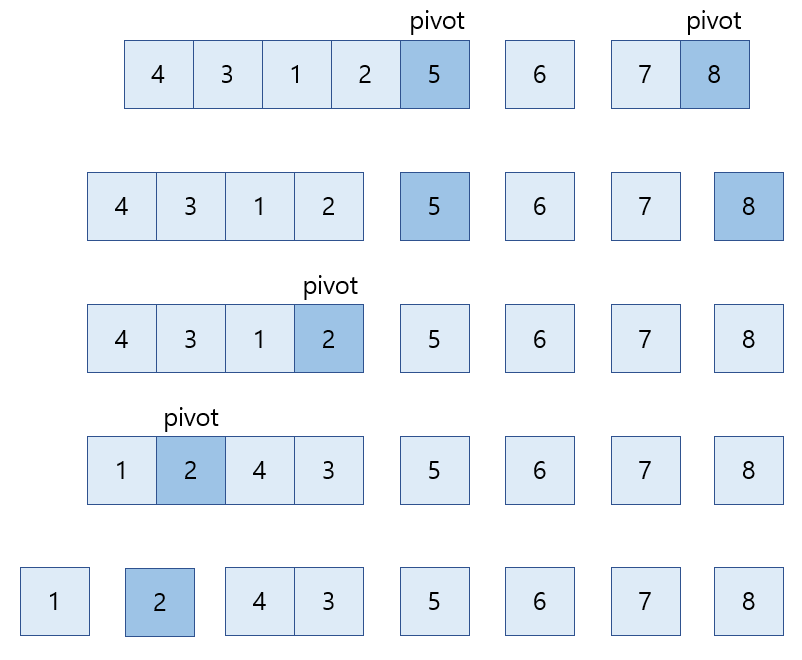
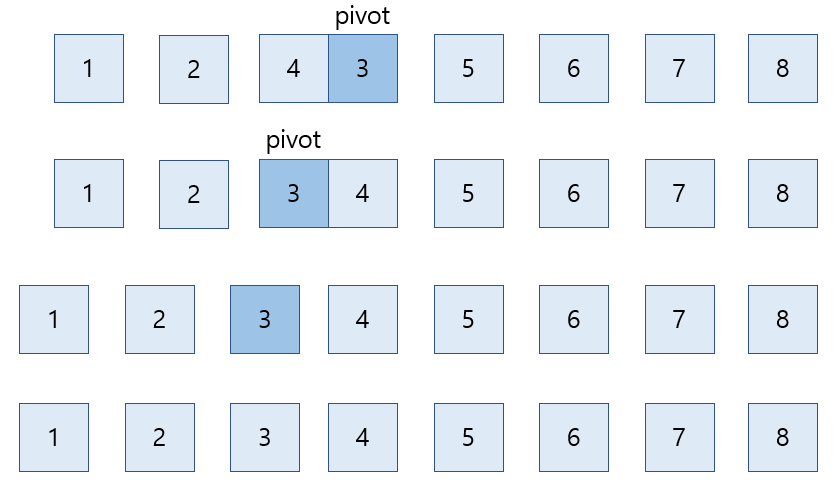
4) 위와 같이 리스트를 분할한 뒤 하위 리스트에도 똑같이 적용
코드
import sys
input = sys.stdin.readline
def quick_sort(lt, rt):
if lt<rt:
p = lt
pivot = arr[rt]
# pivot전까지 순회
for i in range(lt, rt):
# pivot보다 작을 때만 바꿔주고 p증가 시켜줌
if arr[i] <= pivot:
arr[i], arr[p] = arr[p], arr[i]
p += 1
# 순회후 pivot이랑 p 자리 교체
arr[rt], arr[p] = arr[p], arr[rt]
# divide
quick_sort(lt, p-1)
quick_sort(p+1, rt)
if __name__ == "__main__":
arr = [4, 3, 7, 1, 2, 8, 5, 6]
print("정렬전 리스트: ", end='')
print(arr)
quick_sort(0, 7)
print()
print("퀵소트후 리스트: ", end='')
print(arr)
결과
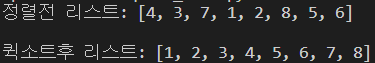
퀵소트는 평균적으로는 O(nlogn)의 시간 복잡도로 준수한 속도를 가지지만, 만약 pivot값이 최소/최댓값으로 지정되어있을 때 O(n^2)의 시간 복잡도를 갖습니다.. ㅜ
(즉, 리스트가 내림차순 또는 오름차순 되어있는 경우)
참고로 파이썬에서 제공하는 sort 함수는 병합정렬 기반이라 O(nlogn)의 시간 복잡도를 갖는다고 하네요!
병합정렬, 퀵정렬 이외에도 다른 정렬들이 있는데 이는 다음에 정렬 파트에서 따로 써보도록 하겠습니다.

'PS > 알고리즘 이론' 카테고리의 다른 글
| [파이썬으로 배우는 알고리즘] Union-Find 알고리즘 (0) | 2022.07.24 |
|---|---|
| [파이썬으로 배우는 알고리즘] 동적 계획법(Dynamic Programming) (0) | 2022.07.22 |
| [파이썬으로 배우는 알고리즘] 그리디(Greedy) 알고리즘 (0) | 2022.07.18 |
| [파이썬으로 배우는 알고리즘] 비트마스크(BitMask) (0) | 2022.07.15 |
| [파이썬으로 배우는 알고리즘] BFS(너비 우선 탐색) (0) | 2022.07.14 |
![[파이썬으로 배우는 알고리즘] 분할정복(Divide & Conquer)과 병합/퀵정렬](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbIJbNO%2FbtrHPKWcQ8E%2FkewLKopiGaiNMvL4SAMQxk%2Fimg.png)