크루스칼(Kruskal) 알고리즘이란?
2022.07.28 - [PS/알고리즘 이론] - [파이썬으로 배우는 알고리즘] 최소 신장 트리(MST)
[파이썬으로 배우는 알고리즘] 최소 신장 트리(MST)
신장 트리 신장 트리(Spanning Tree)란 그래프 내의 모든 노드를 포함하면서 사이클(Cycle)이 없는 부분 그래프를 의미합니다. 이때 모든 노드를 포함하면서 사이클이 없다는 조건은 트리의 성립 조건
c4u-rdav.tistory.com
만약 최소 신장 트리의 개념과 크루스칼 알고리즘의 개념을 모르신다면 위의 포스팅한 글을 보고 간단한 개념을 알고 오시는 게 좋을 것 같습니다!
그리디 알고리즘을 기반으로 최소 신장 트리를 구하는 대표적인 알고리즘이라고 했는데 오늘은 크루스칼 알고리즘을 사용해서 최소 신장 트리를 구하는 세세한 과정과 코드까지 구현해보는 시간을 갖도록 하겠습니다.

크루스칼 알고리즘의 동작 방식

1) 간선의 가중치가 작은 것부터 그래프에 포함시키는 것이기 때문에 모든 간선 정보를 오름차순으로 정렬을 해주고 하나씩 포함시킵니다. 그리고 사이클을 형성하면 안 되기 때문에 루트 테이블로 Union-Find 알고리즘을 사용해 두 노드가 연결되어 있는지(같은 루트 노드를 갖고 있는지) 확인합니다.
2022.07.24 - [PS/알고리즘 이론] - [파이썬으로 배우는 알고리즘] Union-Find 알고리즘
[파이썬으로 배우는 알고리즘] Union-Find 알고리즘
Union-Find의 개념 Union-Find 알고리즘을 알기 위해서는 Disjoint Set의 개념부터 알고 가야 합니다. Disjoint Set이란? Disjoint Set이란 상호배타적인 집합으로 서로 중복되지 않는 부분 집합들로 나눠진 원소
c4u-rdav.tistory.com

2) 첫 번째 간선을 선택합니다. 노드 1과 노드 2는 서로 연결되어 있지 않으므로 연결해주고 1의 루트 노드가 더 작으므로 2의 루트 노드를 1로 바꿔줍니다(바꿔주는 이유 모르시면 Union-Find 알고리즘 글 참고하세요!).

3) 두 번째 간선을 선택합니다. 노드 2와 노드 4는 서로 연결되어 있지 않으므로 연결해주고 2의 루트 노드가 더 작으므로 4의 루트 노드를 1로 바꿔줍니다.
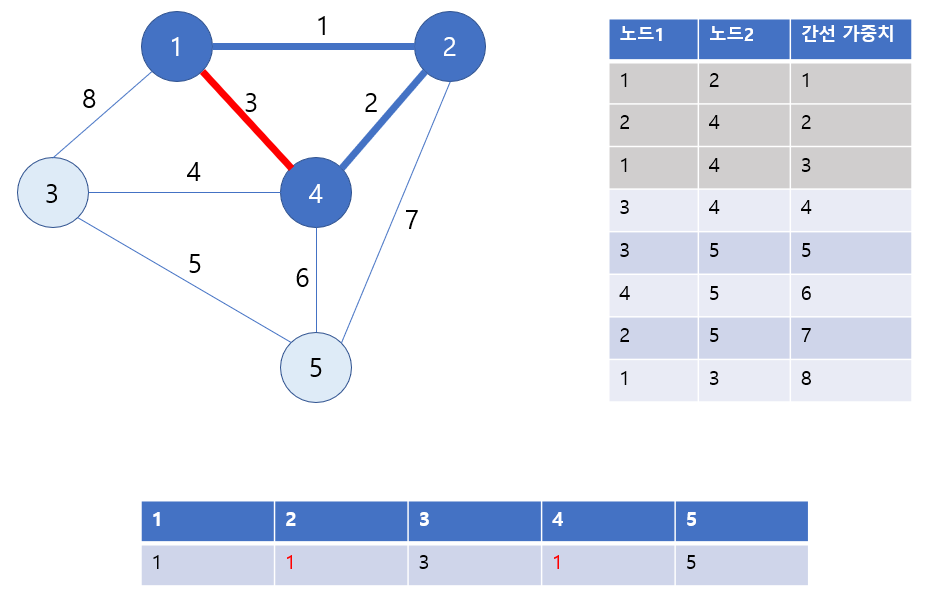
4) 세 번째 간선을 선택합니다. 노드 1과 노드 4는 루트 노드가 같으므로 서로 연결되어 있습니다. 이 간선을 선택하면 사이클을 형성하기 때문에 이 간선은 연결하지 않습니다.
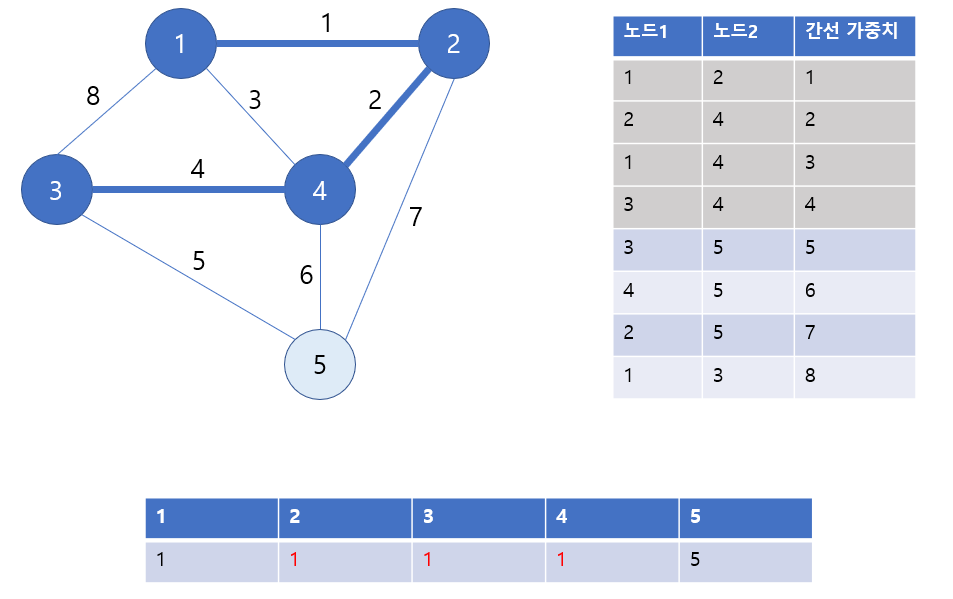
5) 네 번째 간선을 선택합니다. 노드 3과 노드 4는 서로 연결되어 있지 않으므로 연결해주고 4의 루트 노드가 더 작으므로 3의 루트 노드를 1로 바꿔줍니다.
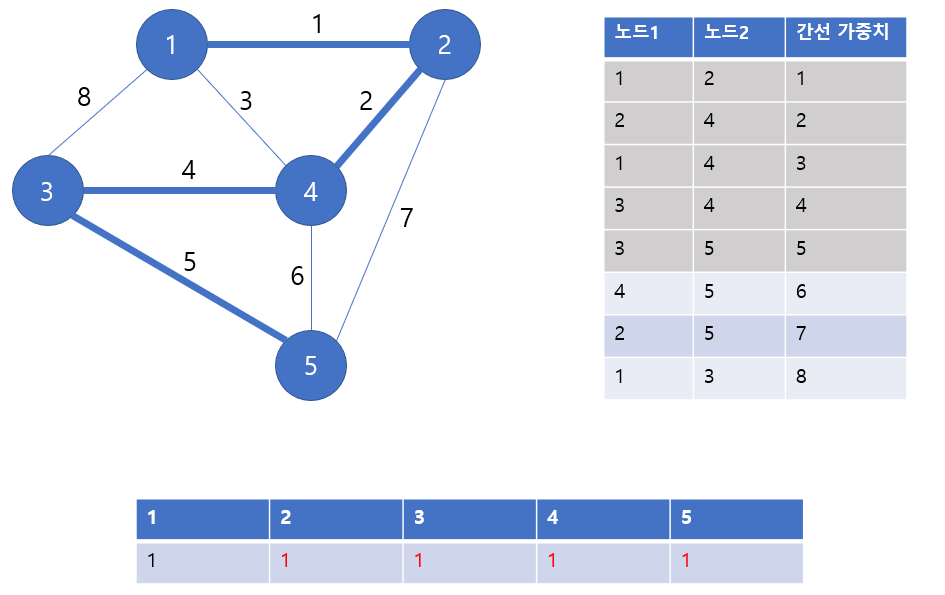
6) 다섯 번째 간선을 선택합니다. 노드3과 노드 5는 서로 연결되어 있지 않으므로 연결해주고 3의 루트 노드가 더 작으므로 5의 루트 노드를 1로 바꿔줍니다.
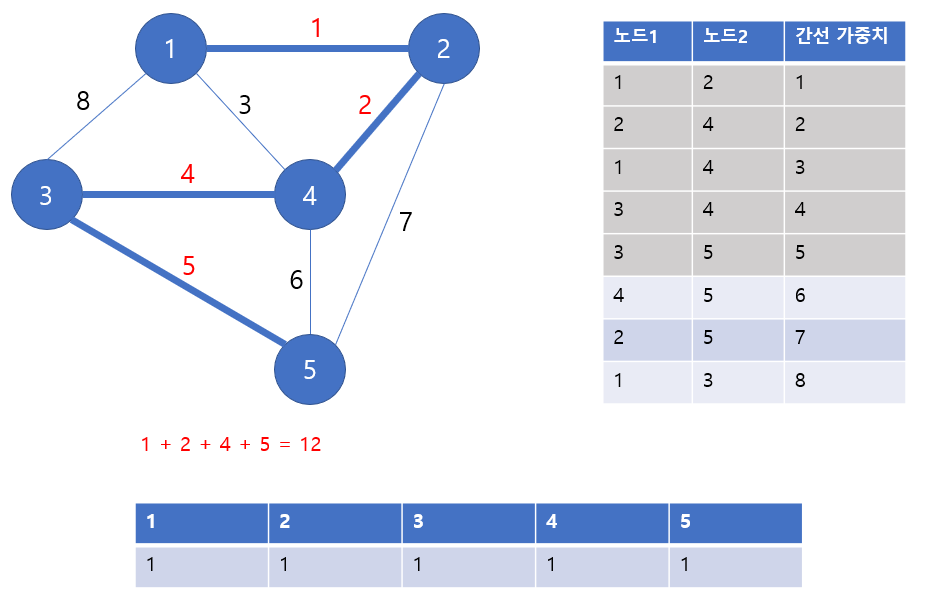
7) 루트 테이블이 모두 1이 되어(& 연결된 간선의 개수 = n-1) 종료해줍니다.
크루스칼 알고리즘 구현
코드
def find(v):
if v != root[v]:
root[v] = find(root[v])
return root[v]
def union(v1, v2):
v1 = find(v1)
v2 = find(v2)
if v1 < v2:
root[v2] = v1
else:
root[v1] = v2
def is_connect(v1, v2):
v1 = find(v1)
v2 = find(v2)
if v1 == v2:
return True
else:
return False
def kruskal():
edge_info = list()
# 간선 정보 저장
for i in range(1, NODE_CNT + 1):
for j in range(i + 1, NODE_CNT + 1):
if graph[i][j] != 0:
edge_info.append((i, j, graph[i][j]))
# 가중치 오름차순 정렬
edge_info.sort(key = lambda x: x[2])
print('#####################')
print('Minimum Spanning Tree')
sum_w = 0
for v1, v2, weight in edge_info:
# 두 노드가 연결되어 있지 않다면
if not is_connect(v1, v2):
sum_w += weight
# 연결
union(v1, v2)
print('Connected Nodes:', v1, v2, 'Weight:', weight)
print('Sum of weight:', sum_w)
print('#####################')
if __name__ == "__main__":
NODE_CNT = 5
graph = [[0] * (NODE_CNT + 1) for _ in range(NODE_CNT + 1)]
root = list(range(NODE_CNT + 1))
graph[1][2], graph[1][3], graph[1][4] = 1, 8, 3
graph[2][1], graph[2][4], graph[2][5] = 1, 2, 7
graph[3][1], graph[3][4], graph[3][5] = 8, 4, 5
graph[4][1], graph[4][2], graph[4][3], graph[4][5] = 3, 2, 4, 6
graph[5][2], graph[5][3], graph[5][4] = 7, 5, 6
kruskal()결과

크루스칼 알고리즘의 시간 복잡도 = O(E log E) (E는 간선의 개수)
모든 간선을 가중치를 기준으로 오름차순 정렬! 정렬 + Union-Find
프림 알고리즘 -> 2022.07.30 - [PS/알고리즘 이론] - [파이썬으로 배우는 알고리즘] 프림(Prim) 알고리즘
[파이썬으로 배우는 알고리즘] 프림(Prim) 알고리즘
프림(Prim) 알고리즘 2022.07.28 - [PS/알고리즘 이론] - [파이썬으로 배우는 알고리즘] 최소 신장 트리(MST) [파이썬으로 배우는 알고리즘] 최소 신장 트리(MST) 신장 트리 신장 트리(Spanning Tree)란 그래프
c4u-rdav.tistory.com

'PS > 알고리즘 이론' 카테고리의 다른 글
| [파이썬으로 배우는 알고리즘] 다익스트라(Dijkstra) 알고리즘 (0) | 2022.07.31 |
|---|---|
| [파이썬으로 배우는 알고리즘] 프림(Prim) 알고리즘 (0) | 2022.07.30 |
| [파이썬으로 배우는 알고리즘] 최소 신장 트리(MST) (0) | 2022.07.28 |
| [파이썬으로 배우는 알고리즘] Union-Find 알고리즘 (0) | 2022.07.24 |
| [파이썬으로 배우는 알고리즘] 동적 계획법(Dynamic Programming) (0) | 2022.07.22 |
![[파이썬으로 배우는 알고리즘] 크루스칼(Kruskal) 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FBCCJX%2FbtrIseuM2Cu%2FGi9pFFLrNckr3R3cyYOAL0%2Fimg.png)