문제
https://www.acmicpc.net/problem/1520
1520번: 내리막 길
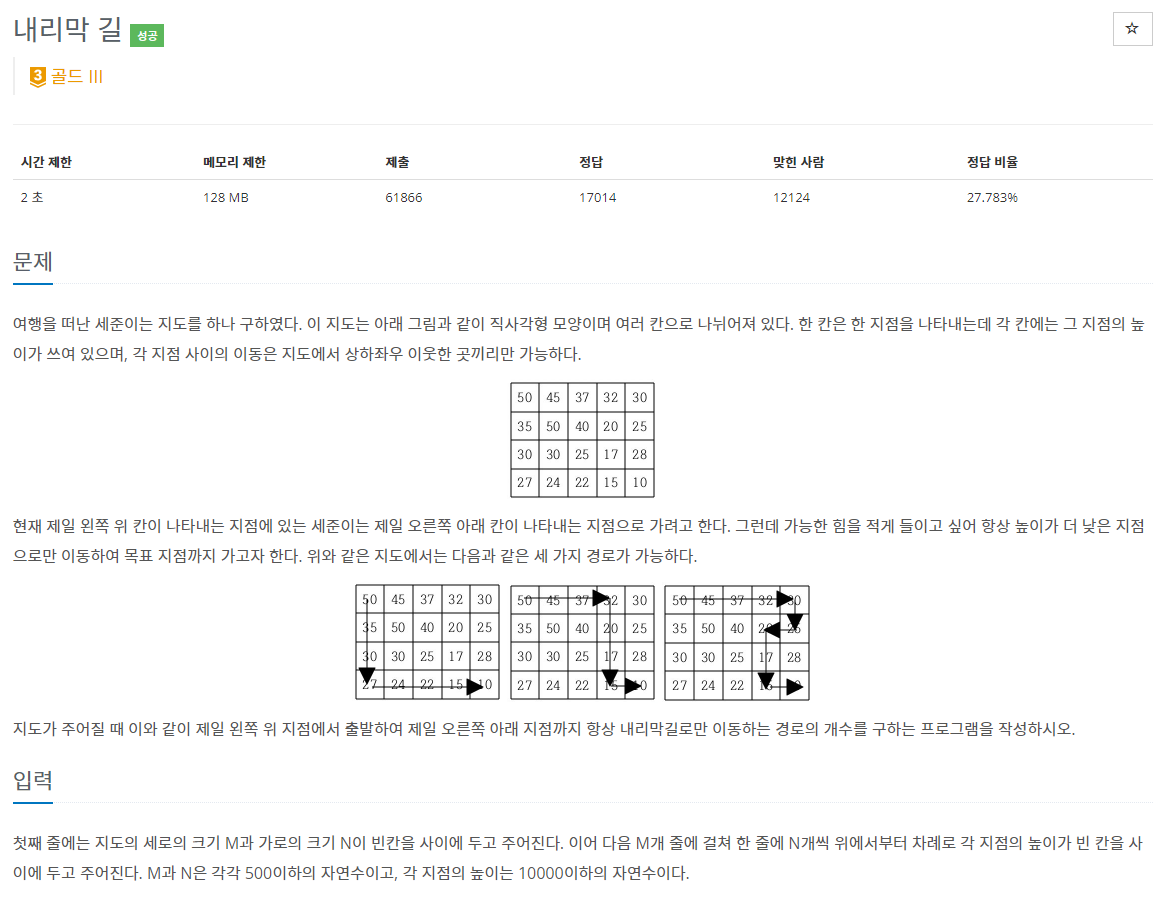
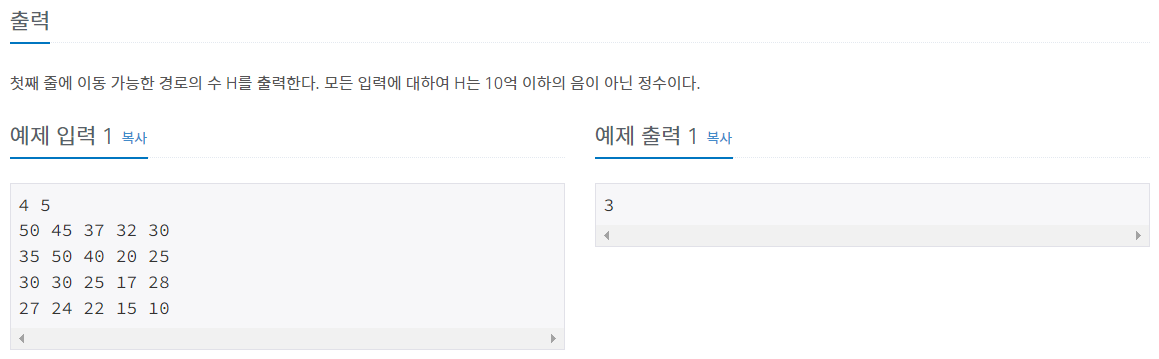
여행을 떠난 세준이는 지도를 하나 구하였다. 이 지도는 아래 그림과 같이 직사각형 모양이며 여러 칸으로 나뉘어져 있다. 한 칸은 한 지점을 나타내는데 각 칸에는 그 지점의 높이가 쓰여 있으
www.acmicpc.net
문제 풀이
DFS + 동적 계획법
2022.07.22 - [PS/알고리즘 이론] - [파이썬으로 배우는 알고리즘] 동적 계획법(Dynamic Programming)
[파이썬으로 배우는 알고리즘] 동적 계획법(Dynamic Programming)
동적 계획법(Dynamic Programming)이란? 동적 계획법(Dynamic Programming), 다이나믹 프로그래밍, DP라고 불리는 이 알고리즘은 무엇일까요?? 동적 프로그래밍? 저는 이 말을 처음 접했을 때 의미에 대해 생
c4u-rdav.tistory.com
2022.07.12 - [PS/알고리즘 이론] - [파이썬으로 배우는 알고리즘] DFS(깊이 우선 탐색)
[파이썬으로 배우는 알고리즘] DFS(깊이 우선 탐색)
DFS란? DFS(Depth First Search)는 그래프의 모든 노드를 탐색하는 방법 중 하나로, 깊이를 우선으로 탐색한 후 더 이상 탐색할 노드가 없다면 이전으로 돌아가 탐색을 이어나가는 탐색 알고리즘입니다.
c4u-rdav.tistory.com
단순히 DFS 알고리즘만 적용시키면 입력이 커서 시간 초과가 발생합니다. 경로의 수를 DFS 알고리즘으로 구할 때 중복된 경로가 존재하는데 동적 계획법을 활용하면 중복된 경로에 대한 연산을 하지 않고, 이미 계산된 경로의 수를 사용하여 연산 횟수를 줄일 수 있습니다.
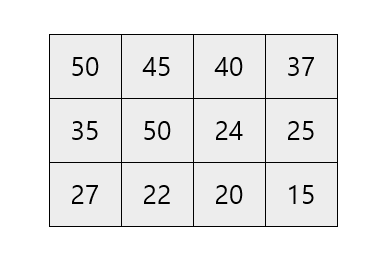
위와 같이 지도가 주어졌을 때 어떻게 동적 계획법을 적용시킬 수 있는지 보겠습니다.
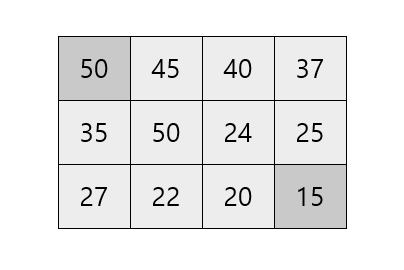
시작 지점은 0, 0이고, 종료 지점은 N-1, M-1입니다.
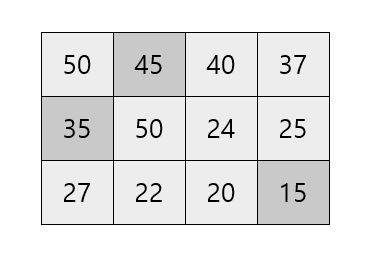
시작 지점 0, 0에서 N-1, M-1까지의 경로의 수는 인접한 1, 0과 0, 1 지점에서의 경로의 수를 합한 것과 같습니다. 나머지 지점에서의 경로의 수도 마찬가지로 방문하지 않은 인접한 지점의 경로의 수를 합한 것과 같고, 이를 dp 테이블에 저장합니다.
이때 dp테이블에서 해당 지점이 방문했을 경우 즉, 경로의 수가 저장되어 있는 경우 추가적인 탐색 연산을 하지 않고, 바로 값을 반환하여 연산 횟수를 줄이게 됩니다.
또한 베이스 케이스로 N-1, M-1 지점에 도달했을 경우 1을 반환하여 목적지까지 이동할 수 있음을 전파합니다.
임의의 지점 x, y로 부터 지점 N-1, M-1까지의 경로의 수를 반환하는 함수를 dfs(x, y)라고 할 때
dfs(x, y)는
탐색하지 않은 x, y 지점에 대해
dp[x][y] += dfs(x, y와 인접하면서 x, y 지점의 높이보다 높이가 낮은 지점)로 dp 테이블을 갱신 후 반환
탐색을 했거나 탐색할 수 없는 경우
dp[x][y]를 그대로 반환
메모이제이션 과정
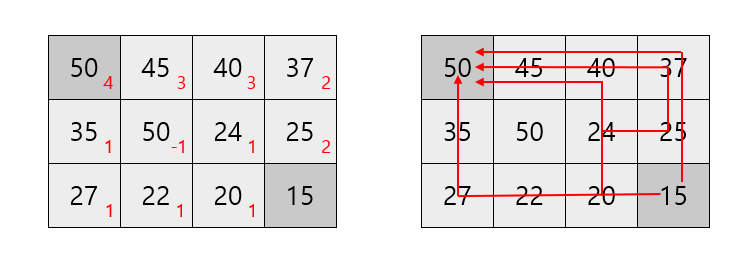
이렇게 DFS와 동적 계획법을 적용하면 위와 같이 dp테이블이 갱신됩니다.
구현
코드
import sys
sys.setrecursionlimit(10 ** 6)
input = sys.stdin.readline
dx = [-1, 0, 1, 0]
dy = [0, 1, 0, -1]
def dfs(tx, ty):
# base case 목적지에 도달 1반환
if tx == N-1 and ty == M-1:
return 1
# 아직 탐색하지 않은 경우
if dp[tx][ty] == -1:
dp[tx][ty] = 0
for k in range(4):
x = tx + dx[k]
y = ty + dy[k]
# 인접하면서 높이가 더 낮은 지점 탐색
if 0 <= x < N and 0 <= y < M and roadmap[tx][ty] > roadmap[x][y]:
dp[tx][ty] += dfs(x, y)
return dp[tx][ty]
if __name__ == "__main__":
N, M = map(int, input().split())
roadmap = [list(map(int, input().split())) for _ in range(N)]
dp = [[-1] * M for _ in range(N)]
print(dfs(0, 0))결과

'PS > 백준' 카테고리의 다른 글
| [백준(BOJ)] #17298- 오큰수 (파이썬, PyPy3) (0) | 2022.11.30 |
|---|---|
| [백준(BOJ)] #4485- 녹색 옷 입은 애가 젤다지? (파이썬, PyPy3) (0) | 2022.11.16 |
| [백준(BOJ)] #10026- 적록색약 (파이썬, Python3) (0) | 2022.11.15 |
| [백준(BOJ)] #2014- 소수의 곱 (파이썬, PyPy3) (0) | 2022.11.12 |
| [백준(BOJ)] #1507- 궁금한 민호 (파이썬, PyPy3) (0) | 2022.11.11 |
![[백준(BOJ)] #1520- 내리막 길 (파이썬, Python3)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FRTRso%2FbtrRjzDzWzO%2FO6maNUrPmHJ7mIHk3iKUyk%2Fimg.png)