그래프(Graph)란?
그래프는 노드(정점)와 간선으로 이루어진 집합으로 표현되는 자료구조입니다.

위 그래프에서 A, B, C는 노드이고, 이 노드를 연결한 선이 간선입니다. 두 노드가 연결되어 있으면 두 노드는 인접하다고 표현됩니다. 따라서 위의 그래프에서는 A, B가 서로 인접하고, A, C가 서로 인접합니다.
또한 그래프는 위 그림과 같이 간선이 방향을 갖고 있지 않는 무방향 그래프, 간선이 방향을 갖고 있는 방향 그래프, 그리고 간선이 가중치를 갖고 있는 가중치 그래프로 나뉩니다.

위의 그래프는 간선이 방향을 갖고 있으므로 방향 그래프입니다. 무방향 그래프처럼 A, B가 모두 연결되어 있는 것이 아니라 A, B를 잇는 간선이 A에서 B 쪽으로 방향을 갖고 있어서 A가 B로는 인접하고, B에서 A로는 인접하지 않습니다. A, C도 마찬가지로 C에서 A로 방향을 갖고 있으므로 C에서 A로는 인접하고 A에서 C로는 인접하지 않습니다.

위의 그래프는 간선이 가중치를 갖고 있는 가중치 그래프입니다. 각 간선에는 가중치 정보가 할당 되어 있고, 네트워크(Network)라고도 불립니다.
그래프 구현
인접 행렬
인접 행렬은 2차원 배열로 그래프의 연결 관계를 표현한 것으로, 파이썬에서는 2차원 리스트를 사용해 인접 행렬을 구현할 수 있습니다.
무방향 그래프의 인접 행렬
| 연결 관계 | A | B | C |
| A | 0 | 1 | 1 |
| B | 1 | 0 | 0 |
| C | 1 | 0 | 0 |
같은 노드와의 연결 관계는 0으로 표시되고, 가중치가 없는 경우 연결 관계만 표현하면 되므로 연결된 노드는 1 연결되지 않은 노드는 0으로 표시됩니다. 무방향 그래프에서는 두 노드 사이에 간선이 존재하면 두 노드는 서로 인접한 것으로 인접 행렬은 대칭이 됩니다.
방향 그래프의 인접 행렬
| 연결 관계 | A | B | C |
| A | 0 | 1 | 0 |
| B | 0 | 0 | 0 |
| C | 1 | 0 | 0 |
무방향 그래프의 인접 행렬과 달리 방향을 갖고 있으므로 대칭적인 모습이 아닙니다. A와 B 사이에 간선이 존재하지만 A에서 B로 방향이 존재하므로 A에서 B는 연결되어 있지만, B에서 A는 연결되지 않았습니다.
가중치 그래프의 인접 행렬
| 연결 관계 | A | B | C |
| A | 0 | 7 | 3 |
| B | 7 | 0 | INF |
| C | 3 | INF | 0 |
마찬가지로 같은 노드와의 연결관계는 0으로 표시되지만, 연결 관계로는 가중치가 표현되므로 연결 되어 있는 경우 가중치 값으로 표현을 하고, 연결되어 있지 않은 경우 무한으로 표현합니다.
가중치 그래프의 인접 행렬 코드 구현
# 정수 최대값으로 무한 표시
INF = 2147000000
# 인접 행렬 0, 1, 2 인덱스 각각 A, B, C 의미
graph = [
[0, 7, 3],
[7, 0, INF],
[3, INF, 0]
]
# A -> B
# 7 출력
print(graph[0][1])
# B -> C
# 2147000000 출력
print(graph[1][2])
인접 리스트
인접 리스트는 연결 관계를 연결된 노드에 대한 정보를 연결하여 저장하는 방식으로 나타냅니다. 인접 행렬과 마찬가지로 파이썬에서는 2차원 리스트로 나타낼 수 있습니다.
무방향 그래프의 인접 리스트
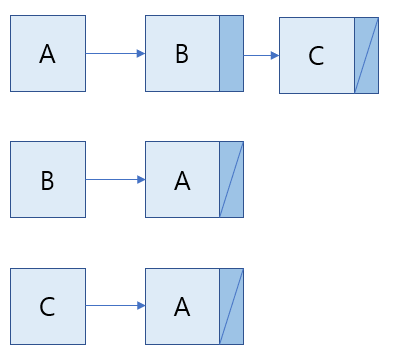
B, C가 A에 연결 되어 있으므로, A의 인접 리스트로 위와 같이 표현이 됩니다. B, C도 마찬가지로 적용시켜주면 됩니다.
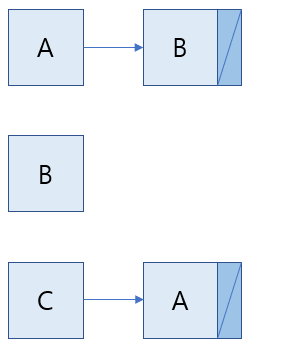
방향 그래프의 인접 리스트
가중치 그래프의 인접 리스트
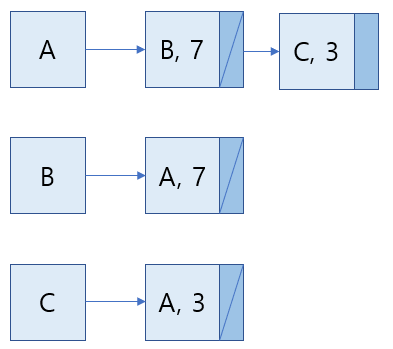
모양은 방향이 없기 때문에 무방향 그래프와 비슷하지만, 가중치 정보도 포함시켜야 합니다.
가중치 그래프의 인접 리스트 구현
# 인접 리스트 0, 1, 2 인덱스 각각 A, B, C 의미
graph = [[] for _ in range(3)]
# A에서 B의 연결을 가중치 7을 포함하여 튜플로 저장
graph[0].append((1, 7))
# A에서 C의 연결을 가중치 3을 포함하여 튜플로 저장
graph[0].append((2, 3))
# B에서 A의 연결을 가중치 7을 포함하여 튜플로 저장
graph[1].append((0, 7))
# C에서 A의 연결을 가중치 3을 포함하여 튜플로 저장
graph[2].append((0, 3))
# A에 연결된 노드 및 가중치 출력
for i in range(len(graph[0])):
print('연결된 노드:', graph[0][i][0], '가중치:', graph[0][i][1])
# 출력
# 연결된 노드: 1 가중치: 7
# 연결된 노드: 2 가중치: 3
두 방식의 장단점
| 인접 행렬 | 인접 리스트 | |
| 장점 | 모든 관계를 저장하기 때문에 두 노드의 연결 정보를 빠르게 탐색할 수 있다. | 연결된 노드에 대한 정보만 저장하기 때문에 간선에 개수에 비례하는 메모리만 차지한다. |
| 단점 | 모든 관계를 저장하기 때문에 그래프에 대한 정보가 커질 수록 메모리 낭비가 심하다. | 두 노드에 대한 연결 정보를 얻는 데 속도가 느리다. |
'CS > 자료구조' 카테고리의 다른 글
| [파이썬으로 배우는 자료구조] 우선순위 큐(Priority Queue), 힙(Heap) (0) | 2022.07.19 |
|---|---|
| [파이썬으로 배우는 자료구조] 트리(Tree) (0) | 2022.07.08 |
| [파이썬으로 배우는 자료구조] 해시(Hash) (0) | 2022.07.03 |
| [파이썬으로 배우는 자료구조] 스택(Stack), 큐(Queue) (0) | 2022.06.29 |
![[파이썬으로 배우는 자료구조] 그래프(Graph)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fb7r4oU%2FbtrGnWRHgf4%2FqP8sdtrYH4CgXXvYdo1wVk%2Fimg.png)