우선순위 큐(Priority Queue)란?
일반적인 큐(Queue) 자료구조는 FIFO 구조라는 것을 배웠습니다.
큐 배우기 --> 2022.06.29 - [CS/자료구조] - [파이썬으로 배우는 자료구조] 스택(Stack), 큐(Queue)
[파이썬으로 배우는 자료구조] 스택(Stack), 큐(Queue)
1. 스택(Stack) 1.1. 스택이란? 스택은 후입선출의 자료구조로 LIFO(Last In First Out)라고 불리기도 합니다. 실생활에서 예를 들어볼까요? 우리가 보통 접시를 선반에 차곡차곡 쌓아올린 후 쌓여있는
c4u-rdav.tistory.com
그렇다면 우선순위 큐는 무엇을 의미할까요??

먼저 들어온 데이터를 무작정 먼저 처리하는 구조가 아니라 데이터에 우선순위에 따라 우선순위가 높은 데이터를 먼저 처리하는 구조를 우선순위 큐(Priority Queue)라고 합니다!
4, 6, 3, 1, 2 순으로 데이터가 들어오고 각각의 숫자를 우선순위라 생각해봅시다.
1) 4가 큐에 들어옵니다. 4는 현재 큐에 있는 데이터 중 우선순위가 제일 높습니다.
2) 6이 큐에 들어옵니다. 6은 4보다 우선순위가 높으므로 6, 4 순서로 정렬해야 우선순위대로 데이터를 처리할 수 있습니다.
3) 3이 큐에 들어옵니다. 3은 앞에 있는 두 데이터보다 우선순위가 낮으므로 큐의 변화가 없습니다.
4) 1이 큐에 들어옵니다. 1도 마찬가지로 앞에 있는 데이터보다 우선순위가 낮으므로 큐의 변화가 없습니다.
5) 2가 큐에 들어옵니다. 2는 1보다 우선순위가 크므로 자리를 바꿔줍니다.
이렇게 우선순위를 고려해 큐에 삽입하면 [6, 4, 3, 2, 1]의 리스트를 얻게 되고, 이를 순서대로 처리하면 우선순위에 맞게 데이터를 처리하는 것입니다.
"아 그럼 데이터를 삽입할 때마다 큐에 있는 데이터를 하나씩 비교해서 우선순위에 맞는 자리를 찾아 넣으면 되겠네!"
구현은 쉽지만 삽입 과정에서 뒤에 위치하게 될 데이터들을 모두 한 칸씩 뒤로 밀어야 한다는 단점이 있습니다. 또한 최악의 경우 삽입해야 하는 위치를 찾기 위해 모든 인덱스를 탐색해야 할 수 있으므로 데이터가 N개라면 O(N)의 시간 복잡도를 갖습니다.
이런 점들을 보완하여 우선순위 큐를 구현할 때는 힙(Heap) 자료구조를 사용합니다.
힙(Heap)이란?
힙은 기본적으로 완전 이진 트리로 이루어져 있습니다.
트리 배우기 --> 2022.07.08 - [CS/자료구조] - [파이썬으로 배우는 자료구조] 트리(Tree)
[파이썬으로 배우는 자료구조] 트리(Tree)
1. 트리(Tree)란? 트리는 노드(Node)와 엣지(Edge)로 구성되어 있습니다. 위 그림에서 원이 노드, 선이 엣지이고, 이를 이용해서 사이클(순환 구조)을 이루지 않도록 구성한 구조를 마치 나무 같다 하
c4u-rdav.tistory.com
또한 모든 노드의 우선순위가 자식 노드의 우선순위보다 크거나 같으며, 우선순위의 기준을 어떻게 잡느냐에 따라서 최소힙과, 최대힙으로 나뉩니다.
최대힙(Max Heap)

값이 클수록 우선순위가 높으며 힙의 성질에 따라 루트 노드로 올라갈수록 값이 커짐. (부모 노드 >= 자식 노드)
최소힙(Min Heap)
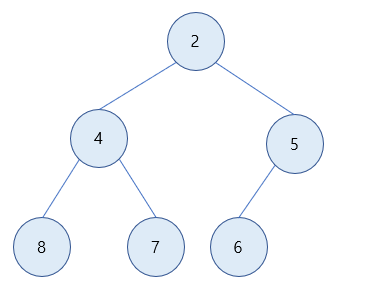
값이 작을수록 우선순위가 높으며 힙의 성질에 따라 루트 노드로 올라갈수록 값이 작아짐. (부모 노드 <= 자식 노드)
힙의 동작
최소힙으로 힙에서 삽입, 삭제는 어떻게 동작하는지 알아보도록 해요!
삽입
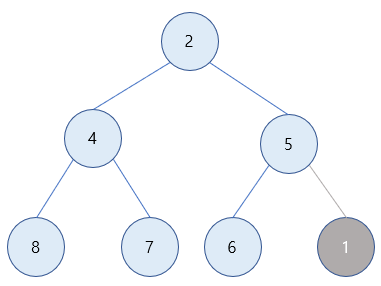
1) 1을 최소힙에 삽입한다고 할게요. 위에서 말했듯이 힙은 완전 이진 트리로 이루어져 있으므로 삽입을 할 때에도 이를 유지해야 합니다. 따라서 완전 이진 트리를 만족하는 자리에 1 값의 노드가 삽입이 됩니다.
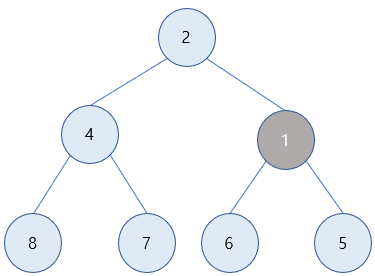
2) 1은 값이 5인 부모 노드보다 값이 작으므로 최소 힙의 성질을 만족하기 위해 부모 노드와 자리를 바꿔줍니다.
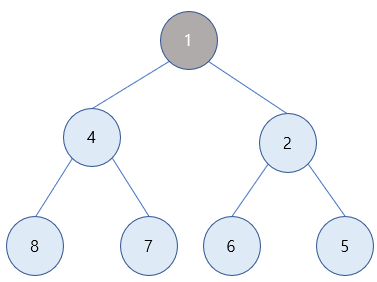
3) 마찬가지로 1은 값이 2인 부모노드보다 값이 작으므로 최소힙의 성질을 만족하기 위해 부모 노드와 자리를 바꿔줍니다.
이렇게 삽입이 완료됩니다.
삭제
최소 힙에서의 삭제는 값이 제일 작은 노드 즉, 루트 노드의 삭제를 의미합니다.
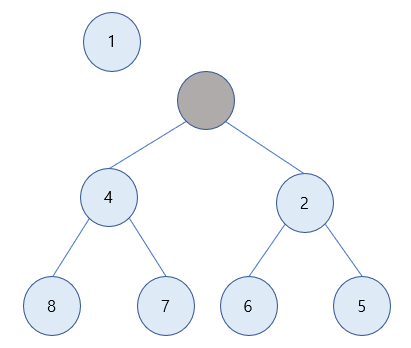
1) 위와 같이 1 값을 가진 노드가 삭제됩니다.
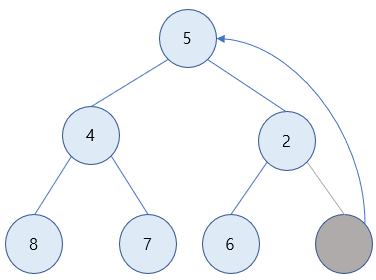
2) 루트 노드가 비게 되며, 이를 마지막 노드가 채우게 됩니다.
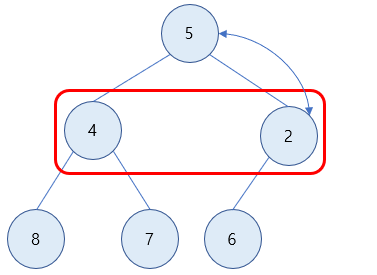
3) 자식 노드가 값이 더 작으므로 값을 교환해주기 위해 더 작은 값을 구합니다. 2가 4보다 더 작으므로 2의 값을 가진 노드와 루트 노드의 자리를 바꿉니다.
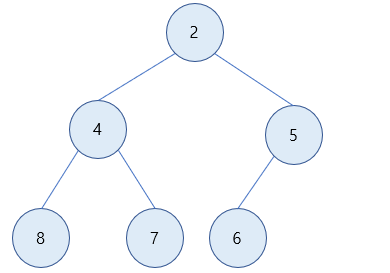
4) 최소힙을 만족하여 삭제가 종료됩니다.
삽입, 삭제는 트리의 높이까지 비교가 이루어지기 때문에 데이터가 N 개라면 O(logN)의 시간 복잡도를 갖습니다.
또한 파이썬에서는 heapq라는 라이브러리를 지원하여 힙을 직접 구현하지 않고 라이브러리로 사용할 수도 있습니다.

힙 구현
최소힙 직접 구현
코드
class Heap:
def __init__(self):
self.heap = []
# 삽입하고 최소힙 만족하기 위한 부모노드 탐색
def check_with_parent(self, index):
if index == 0:
return False
else:
# 부모 노드 인덱스
parent_index = (index - 1) // 2
if self.heap[parent_index] > self.heap[index]:
return True
return False
# 삽입
def push(self, value):
self.heap.append(value)
index = len(self.heap)-1
while self.check_with_parent(index):
parent = (index - 1) // 2
self.heap[index], self.heap[parent] = self.heap[parent], self.heap[index]
index = (index - 1) // 2
# 삭제하고 최소힙 만족하기 위한 자식 노드 탐색
def check_with_child(self, index):
# 자식 노드 인덱스
left_child = 2 * (index+1) - 1
right_child = 2 * (index+1)
last_index = len(self.heap) - 1
# 왼쪽 자식 노드만 있는 경우
if left_child <= last_index and right_child > last_index:
if self.heap[left_child] <= self.heap[index]:
return (True, 1)
else:
return (False, -1)
# 오른쪽 자식 노드만 있는 경우
elif left_child > last_index and right_child <= last_index:
if self.heap[right_child] <= self.heap[index]:
return (True, 2)
else:
return (False, -1)
# 둘다 있는 경우
elif left_child <= last_index and right_child <= last_index:
if self.heap[left_child] > self.heap[index] and self.heap[right_child] > self.heap[index]:
return (False, -1)
else:
if self.heap[left_child] <= self.heap[index]:
return (True, 3)
else:
return (True, 4)
return (False, -1)
# 삭제
def pop(self):
if not self.heap:
return None
else:
res = self.heap[0]
self.heap[0] = self.heap[-1]
self.heap.pop()
index = 0
while self.check_with_child(index)[0]:
p = self.check_with_child(index)[1]
if p == 1 or p == 3:
left_child = 2 * (index+1) - 1
self.heap[index], self.heap[left_child] = self.heap[left_child], self.heap[index]
index = 2 * (index+1) - 1
elif p == 2 or p == 4:
right_child = 2 * (index+1)
self.heap[index], self.heap[right_child] = self.heap[right_child], self.heap[index]
index = 2 * (index+1)
return res
if __name__ == "__main__":
h = Heap()
h.push(3)
h.push(6)
h.push(2)
h.push(10)
h.push(5)
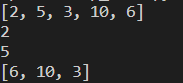
print(h.heap)
print(h.pop())
print(h.pop())
print(h.heap)결과
heapq 라이브러리 사용
코드
import heapq as hq
if __name__ == "__main__":
a = list()
hq.heappush(a, 3)
hq.heappush(a, 6)
hq.heappush(a, 2)
hq.heappush(a, 10)
hq.heappush(a, 5)
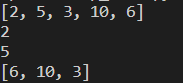
print(a)
print(hq.heappop(a))
print(hq.heappop(a))
print(a)결과
'CS > 자료구조' 카테고리의 다른 글
| [파이썬으로 배우는 자료구조] 트리(Tree) (0) | 2022.07.08 |
|---|---|
| [파이썬으로 배우는 자료구조] 그래프(Graph) (0) | 2022.07.04 |
| [파이썬으로 배우는 자료구조] 해시(Hash) (0) | 2022.07.03 |
| [파이썬으로 배우는 자료구조] 스택(Stack), 큐(Queue) (0) | 2022.06.29 |
![[파이썬으로 배우는 자료구조] 우선순위 큐(Priority Queue), 힙(Heap)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbvFkeS%2FbtrHIkWS2QJ%2FYGn2dJ8aefxkNSsw9epKu0%2Fimg.png)