플로이드 워셜(Floyd Warshall) 알고리즘이란?
플로이드 워셜(Floyd Warshall) 알고리즘은 최단 경로 알고리즘이지만 그래프에서 특정한 노드에서 다른 모든 노드까지의 최단 경로를 구하는 다익스트라 알고리즘과 달리 모든 정점으로부터 모든 정점까지의 최단 경로를 구하는 알고리즘입니다. 플로이드 워셜 알고리즘은 다익스트라 알고리즘과 마찬가지로 동적 계획법을 활용한 알고리즘입니다.
2022.07.31 - [PS/알고리즘 이론] - [파이썬으로 배우는 알고리즘] 다익스트라(Dijkstra) 알고리즘
[파이썬으로 배우는 알고리즘] 다익스트라(Dijkstra) 알고리즘
다익스트라(Dijkstra) 알고리즘이란? 다익스트라(Dijkstra) 알고리즘은 최단 경로 알고리즘으로 그래프에서 특정한 노드에서 다른 모든 노드까지의 최단 경로를 구하는 알고리즘입니다. 그리디 알고
c4u-rdav.tistory.com
플로이드 워셜 알고리즘의 동작
동작 설명
1) 인접 행렬로 그래프를 표시(초기 연결되어 있지 않은 노드와의 관계는 INF로 표시)
2) 인접행렬을 이용하여 특정한 노드를 경유하여 가는 거리 값이 기존 거리 값보다 더 작을 경우 갱신해줌.
3) 모든 노드를 경유한 경우를 고려해야 하기 때문에 모든 노드에 대해 2번 작업 반복
동작 예시

1) 위와 같은 가중치 그래프와 그래프를 나타내는 인접 행렬을 준비합니다. 인접 행렬은 adj_matrix라고 칭하겠습니다.

2) 1을 경유하여 가는 거리를 고려합니다.
1을 포함하는 행과 열을 제외하고 1을 경유하여 가는 거리를 고려하게 됩니다.
노드 2와 3까지의 최단 거리 즉, adj_matrix[2][3] = 2는 1을 경유하여 가는 거리인 adj_matrix[2][1](노드 2와 1의 최단 거리) + adj_matrix[1][3](노드 1과 3의 최단 거리) = 6보다 작으므로 본래의 값을 유지합니다. 해당 그래프는 무방향 그래프로 대칭 행렬이므로 adj_matrix[3][2]에도 똑같이 적용합니다.
노드 2와 4까지의 최단 거리 즉, adj_matrix[2][4] = 8은 1을 경유하여 가는 거리인 adj_matrix[2][1] + adj_matrix[1][4] = INF보다 작으므로 본래의 값을 유지합니다. adj_matrix[4][2]에도 똑같이 적용합니다.
노드 3과 4까지의 최단 거리 즉, adj_matrix[3][4] = 2는 1을 경유하여 가는 거리인 adj_matrix[3][1] + adj_matrix[1][4] = INF보다 작으므로 본래의 값을 유지합니다. adj_matrix[4][3]에도 똑같이 적용합니다.
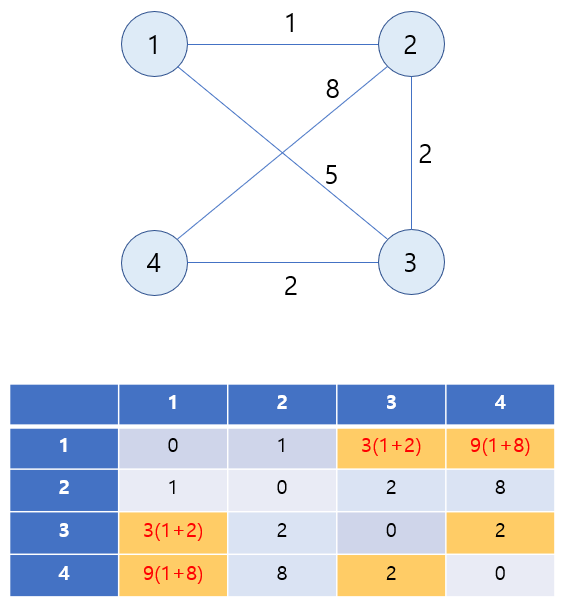
3) 2를 경유하여 가는 거리를 고려합니다.
2를 포함하는 행과 열을 제외하고 2를 경유하여 가는 거리를 고려하게 됩니다.
노드 1과 3까지의 최단 거리 즉, adj_matrix[1][3] = 5는 2를 경유하여 가는 거리인 adj_matrix[1][2](노드 1과 2의 최단 거리) + adj_matrix[2][3](노드 2와 3의 최단 거리) = 3보다 크므로 경유하는 거리로 값을 갱신합니다. 해당 그래프는 무방향 그래프로 대칭 행렬이므로 adj_matrix[3][1]에도 똑같이 적용합니다.
노드 1과 4까지의 최단 거리 즉, adj_matrix[1][4] = INF는 2를 경유하여 가는 거리인 adj_matrix[1][2] + adj_matrix[2][4] = 9보다 크므로 경유하는 거리로 값을 갱신합니다. adj_matrix[4][1]에도 똑같이 적용합니다.
노드 3과 4까지의 최단 거리 즉, adj_matrix[3][4] = 2는 2를 경유하여 가는 거리인 adj_matrix[3][2] + adj_matrix[2][4] = 10보다 작으므로 본래의 값을 유지합니다. adj_matrix[4][3]에도 똑같이 적용합니다.
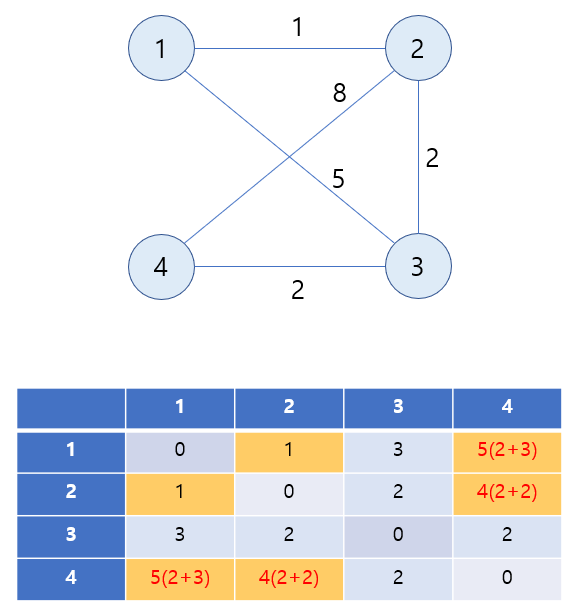
4) 3을 경유하여 가는 거리를 고려합니다.
3을 포함하는 행과 열을 제외하고 3을 경유하여 가는 거리를 고려하게 됩니다.
노드 1과 2까지의 최단 거리 즉, adj_matrix[1][2] = 1은 3을 경유하여 가는 거리인 adj_matrix[1][3](노드 1과 3의 최단 거리) + adj_matrix[3][2](노드 3과 2의 최단 거리) = 5보다 작으므로 본래의 값을 유지합니다. 해당 그래프는 무방향 그래프로 대칭 행렬이므로 adj_matrix[2][1]에도 똑같이 적용합니다.
노드 1과 4까지의 최단 거리 즉, adj_matrix[1][4] = 9는 3을 경유하여 가는 거리인 adj_matrix[1][3] + adj_matrix[3][4] = 5보다 크므로 경유하는 거리로 값을 갱신합니다. adj_matrix[4][1]에도 똑같이 적용합니다.
노드 2와 4까지의 최단 거리 즉, adj_matrix[2][4] = 8은 3을 경유하여 가는 거리인 adj_matrix[2][3] + adj_matrix[3][4] = 4보다 크므로 경유하는 거리로 값을 갱신합니다. adj_matrix[4][2]에도 똑같이 적용합니다.
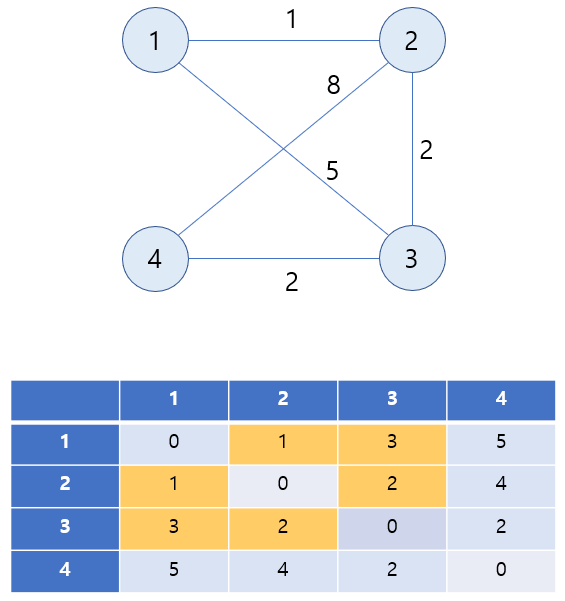
5) 4를 경유하여 가는 거리를 고려합니다.
4를 포함하는 행과 열을 제외하고 4를 경유하여 가는 거리를 고려하게 됩니다.
노드 1과 2까지의 최단 거리 즉, adj_matrix[1][2] = 1은 4를 경유하여 가는 거리인 adj_matrix[1][4](노드 1과 4의 최단 거리) + adj_matrix[4][2](노드 4와 2의 최단 거리) = 9보다 작으므로 본래의 값을 유지합니다. 해당 그래프는 무방향 그래프로 대칭 행렬이므로 adj_matrix[2][1]에도 똑같이 적용합니다.
노드 1과 3까지의 최단 거리 즉, adj_matrix[1][3] = 3은 4를 경유하여 가는 거리인 adj_matrix[1][4] + adj_matrix[4][3] = 7보다 작으므로 본래의 값을 유지합니다. adj_matrix[3][1]에도 똑같이 적용합니다.
노드 2와 3까지의 최단 거리 즉, adj_matrix[2][3] = 2는 4를 경유하여 가는 거리인 adj_matrix[2][4] + adj_matrix[4][3] = 6보다 작으므로 본래의 값을 유지합니다. adj_matrix[3][2]에도 똑같이 적용합니다.

6) 모든 노드에 대하여 모든 노드로의 최단 경로를 얻게 됩니다.
플로이드 워셜 알고리즘 구현
코드
def floyd():
# k는 경유하는 노드
for k in range(1, NODE_CNT + 1):
for i in range(1, NODE_CNT + 1):
for j in range(1, NODE_CNT + 1):
# k노드를 경유하는 거리값이 더 작으면 갱신
graph[i][j] = min(graph[i][j], graph[i][k] + graph[k][j])
if __name__ == "__main__":
NODE_CNT = 4
INF = 2147000000
graph = [[INF] * (NODE_CNT + 1) for _ in range(NODE_CNT + 1)]
for i in range(1, NODE_CNT + 1):
graph[i][i] = 0
graph[1][2] = 1
graph[2][1] = 1
graph[1][3] = 5
graph[3][1] = 5
graph[2][3] = 2
graph[3][2] = 2
graph[2][4] = 8
graph[4][2] = 8
graph[3][4] = 2
graph[4][3] = 2
floyd()
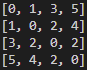
for x in graph[1:]:
print(x[1:])결과
시간 복잡도
그래프의 노드의 개수가 N 개라고 했을 때 경유하는 노드 N개에 대해 N x N 행렬을 갱신해 주어야 하므로 O(N ^ 3)의 시간 복잡도를 갖습니다.

'PS > 알고리즘 이론' 카테고리의 다른 글
| [파이썬으로 배우는 알고리즘] 이분 탐색(Binary Search) (0) | 2022.08.11 |
|---|---|
| [파이썬으로 배우는 알고리즘] 위상 정렬(Topology Sort) (2) | 2022.08.08 |
| [파이썬으로 배우는 알고리즘] 다익스트라(Dijkstra) 알고리즘 (0) | 2022.07.31 |
| [파이썬으로 배우는 알고리즘] 프림(Prim) 알고리즘 (0) | 2022.07.30 |
| [파이썬으로 배우는 알고리즘] 크루스칼(Kruskal) 알고리즘 (0) | 2022.07.29 |
![[파이썬으로 배우는 알고리즘] 플로이드 워셜(Floyd Warshall) 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FChqVr%2FbtrIC0DSROe%2FKYrgTThFAXG4uIEJyycscK%2Fimg.png)