이분 탐색(Binary Search)이란?
이분 탐색(Binary Search)이란 탐색 범위를 절반으로 나눠가며 데이터를 탐색하는 방법입니다. 우리가 흔히 알고 있는 순차 탐색(Linear Search)은 데이터를 앞에서부터 하나씩 탐색하여 시간 복잡도가 O(N)(N은 데이터의 개수)으로 그렇게 효율적인 탐색 방법은 아닙니다. 하지만 이분 탐색은 데이터의 범위를 절반씩 계속 나눠 탐색하기 때문에 시간 복잡도가 O(logN)으로 순차 탐색보다는 훨씬 효율적인 탐색 알고리즘이라고 볼 수 있습니다.
하지만 데이터가 속해 있는 범위를 알아야 하기 때문에 정렬되어 있는 데이터에서만 이분 탐색을 사용할 수 있습니다. 그러면 이분 탐색이 어떻게 사용되는지 순차 탐색과 어떻게 다른지 과정을 보며 확인해보겠습니다.
이분 탐색과 순차 탐색의 비교

위와 같은 데이터 집합에서 13을 찾는다고 가정해봅시다.


먼저 순차 탐색을 적용하면 위와 같이 총 7번의 단계에 거쳐 13이라는 데이터를 찾을 수 있습니다. 만약 13이 아닌 22를 찾는 거였으면 데이터를 처음부터 끝까지 모두 탐색하기 때문에 데이터의 크기가 커질수록 탐색 시간이 느려지게 됩니다. 이번엔 이분 탐색을 적용해보겠습니다.

이분 탐색은 데이터의 범위를 절반씩 줄여나가기 때문에 중간 위치에서 탐색을 시작합니다. 중간에 위치한 데이터는 11입니다. 모두 정렬된 데이터라는 점에서 이제 찾으려는 데이터 13의 범위를 알 수 있습니다. 13은 11보다 크기 때문에 절반을 나눈 데이터의 범위에서 11보다 큰 값들만 있는 오른쪽 범위로 같은 방식으로 탐색을 하게 됩니다.

오른쪽 데이터의 집합에서의 중간 위치인 17을 탐색합니다. 이번에 13은 17보다 작기 때문에 절반을 나눈 데이터의 범위에서 17보다 작은 값들만 있는 왼쪽 범위로 똑같이 탐색을 하게 됩니다.

왼쪽 데이터의 집합에서의 중간 위치인 13을 탐색합니다. 13을 찾았기 때문에 종료합니다. 순차 탐색과 달리 총 3번의 단계에 거쳐 탐색을 완료한 것을 확인할 수 있습니다. 만약 데이터의 크기가 아주 커질 경우 탐색 속도의 차이도 확연해집니다. 이제 직접 코드를 작성해 구현해보겠습니다.
구현
코드
if __name__ == "__main__":
DATA_SIZE = 11
data_list = [1, 3, 5, 8, 9, 11, 13, 15, 17, 20, 22]
target_num = 13
lt = 0
rt = DATA_SIZE - 1
step = 0
position = -1
# 데이터의 오른쪽 인덱스가 왼쪽 인덱스보다 클 때만
while lt <= rt:
step += 1
# 중간 인덱스
mid = (lt + rt) // 2
# 중간 값이 찾고자 하는 숫자보다 크면
if data_list[mid] > target_num:
# 왼쪽 탐색
rt = mid - 1
# 중간 값이 찾고자 하는 숫자보다 작으면
elif data_list[mid] < target_num:
# 오른쪽 탐색
lt = mid + 1
# 중간 값이 찾고자 하는 숫자와 같으면
else:
# 해당 위치 저장후 while문 종료
position = mid
break
print('###############################################')
print("data =", data_list)
print('binary search steps to search', str(target_num)+':', step)
print('position of', str(target_num)+':', position)
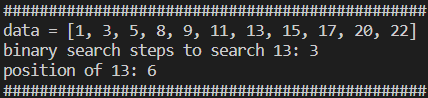
print('###############################################')결과
'PS > 알고리즘 이론' 카테고리의 다른 글
| [파이썬으로 배우는 알고리즘] 선택 정렬(Selection Sort) (0) | 2022.11.17 |
|---|---|
| [파이썬으로 배우는 알고리즘] 버블 정렬(Bubble Sort) (2) | 2022.11.04 |
| [파이썬으로 배우는 알고리즘] 위상 정렬(Topology Sort) (2) | 2022.08.08 |
| [파이썬으로 배우는 알고리즘] 플로이드 워셜(Floyd Warshall) 알고리즘 (0) | 2022.08.01 |
| [파이썬으로 배우는 알고리즘] 다익스트라(Dijkstra) 알고리즘 (0) | 2022.07.31 |
![[파이썬으로 배우는 알고리즘] 이분 탐색(Binary Search)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FnAdaS%2FbtrJo2gIgkM%2FOt60kfvExaZsLl3uk092h0%2Fimg.png)